机器学习入门。
What is Machine Learning
机器学习致力于研究通过计算的手段,利用经验来改善系统自身的性能。在计算机系统中,经验通常以数据形式存在,而机器学习所研究的主要内容,是关于在计算机上从数据中产生模型(Model)的算法,即学习算法(Learning Algorithm)。有了学习算法,把经验数据提供给它,它就能基于这些数据产生模型;在面对新的情况时,模型会给我们提供相应的判断。如果说计算机科学是研究关于算法的学问,那么机器学习就是研究关于学习算法的学问。
Data Set
假定我们收集了一批关于西瓜的数据,例如 (色泽=青绿, 根蒂=蜷缩, 敲声=浊响), (色泽=乌黑, 根蒂=稍蜷, 敲声=沉闷), (色泽=浅白, 根蒂=硬挺, 敲声=清脆)……,这组记录的集合被称作一个数据集(Data Set),其中每条记录是关于一个事件或对象的描述,称为一个示例(Instance)或样本(Sample)。反映事件或对象在某方面的表现或性质的事项,例如色泽、根蒂、敲声,称为属性(Attribute)或特征(Feature);属性上的取值,例如青绿、乌黑,称为属性值(Attribute Value)。属性张成的空间称为属性空间(Attribute Space)、样本空间(Sample Space)或输入空间。如果将色泽、根蒂、敲声作为三个坐标轴,则它们张成一个用于描述西瓜的三维空间,每个西瓜都可在这个空间中找到自己的坐标位置。由于空间中的每个点对应一个坐标向量,因此我们也把一个示例称为一个特征向量(Feature Vector)。
一般地,令 $D=\{x_1,x_2,\cdots,x_m\}$ 表示包含 $m$ 个示例的数据集,每个示例由 $d$ 个属性描述,则每个示例 $x_i=(x_{i1};x_{i2};\cdots;x_{id})$ 是 $d$ 维空间 $\chi$ 中的一个向量,$x_i\in\chi$,其中 $x_{ij}$ 是 $x_i$ 在第 $j$ 个属性上的取值,$d$ 称为样本 $x_i$ 的维数(Dimensionality)。
Training
从数据中学得模型的过程称为学习(Learning)或训练(Training),这个过程通过执行某个学习算法来完成。训练过程中使用的数据称为训练数据(training data),其中每个样本称为一个训练样本(Training Sample),训练样本组成的集合称为训练集(Training Set)。学得模型对应了关于数的某种潜在的规律,因此亦称假设(Hypothesis);这种潜在规律自身,则称为真相或真实(Ground-truth),学习过程就是为了找出或逼近真相。
如果希望学得一个能帮助判断的模型,仅有前面的示例数据是不够的。建立这样的关于预测(Prediction)的模型,我们需获得训练样本的结果信息,例如 ((色泽=青绿, 根蒂=蜷缩, 敲声=浊响), 好瓜)。这里关于示例结果的信息,例如好瓜,称为标记(Label);拥有了标记信息的示例,则称为样例(Example)。一般地,用 $(x_i, y_i)$ 表示第 $i$ 个样例,其中 $y_i\in\upsilon$ 是示例 $x_i$ 的标记,$\upsilon$ 是所有标记的集合,亦称标记空间(Label Space)或输出空间。
若欲预测的是离散值,例如好瓜或坏瓜,此类学习任务称为分类(Classification);若欲预测的是连续值,例如西瓜成熟度,此类学习任务称为回归(Regression)。对只涉及两个类别的二分类(Binary Classification)任务,通常称其中一个类为正类(Positive Class),另一个类为反类(Negative Class);涉及多个类别时,则称为多分类(Multi-class Classification)任务。一般地,预测任务是希望通过对训练集 $\{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\}$ 进行学习,建立一个从输入空间 $\chi$ 到输出空间 $\upsilon$ 的映射 $f:\chi\mapsto\upsilon$。对二分类任务,通常令 $\upsilon = \{-1,+1\}$ 或 $\{0,1\}$;对多分类任务,$\vert\upsilon\vert>2$;对回归任务,$\upsilon=\mathbb{R}$,$\mathbb{R}$ 为实数集。
Testing
学得模型后,使用其进行预测的过程称为测试(Testing),被预测的样本称为测试样本(Testing Sample)。例如在学得 $f$ 后,对测试例 $x$,可得到其预测标记 $y=f(x)$。还可以做聚类(Clustering),即将训练集中的数据分成若干组,每组称为一个簇(Cluster);这些自动形成的簇可能对应一些潜在的概念划分,有助于我们了解数据内在的规律,能为更深入地分析数据建立基础。
根据训练数据是否拥有标记信息,学习任务可大致划分为两大类监督学习(Supervised Learning)和无监督学习(Unsupervised Learning),分类和回归是前者的代表,而聚类则是后者的代表。
机器学习的目标是使学得的模型能很好地适用于新样本,而不是仅仅在训练样本上工作得很好;即便对聚类这样的无监督学习任务,也希望学得的簇划分能适用于没在训练集中出现的样本。学得模型适用于新样本的能力,称为泛化(Generalization)能力。具有强泛化能力的模型能很好地适用于整个样本空间。尽管训练集通常只是样本需间的一个很小的采样,我们仍希望它能很好地反映出样本空间的特性,否则就很难期望在训练集上学得的模型能在整个样本空间上都工作得很好。通常假设样本空间中全体样本服从一个未知分布(Distribution)$D$,我们获得的每个样本都是独立地从这个分布上采样获得的,即独立同分布(Independent and Identically Distributed,简称 I.I.D.)。一般而言,训练样本越多,我们得到的关于 $D$ 的信息越多,这样就越有可能通过学习获得具有强泛化能力的模型。
No Free Lunch Theorem
如果我们不对特征空间有先验假设,则所有算法的平均表现是一样的。
假设有两种算法 $Z_a$ 和 $Z_b$,分别对样本进行测试。得到的结果是不确定的,可能 $Z_a$ 的泛化能力更强,当然也有可能 $Z_b$ 的泛化能力更强。
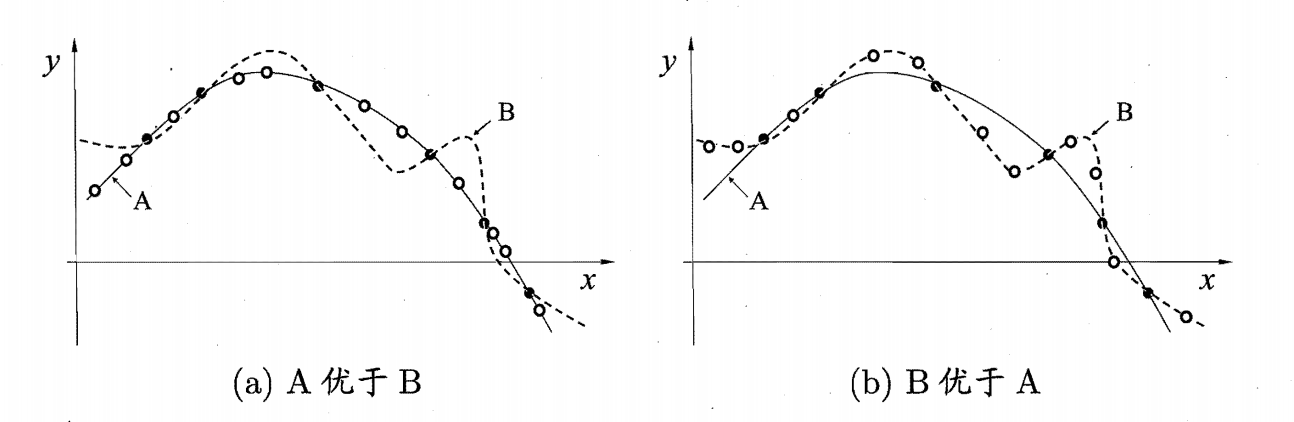
假设样本空间 $\chi$ 和假设空间 $\eta$ 都是离散的。令 $P(h|X, Z_a)$ 代表算法 $Z_a$ 基于训练数据 $X$ 产生假设 $h$ 的概率,再令 $f$ 代表我们希望学习的真实目标函数。$Z_A$ 的训练集外误差,即 $Z_a$ 在训练集之外的所有样本上的误差为:
$$
E_{ote}(Z_A|X,f)=\sum_h\sum_{x\in\chi-X}P(x) {II}(h(x)\not ={f(x)}) P(h|X,Z_a)
$$
其中 $II(\cdot)$ 是指示函数,若 $\cdot$ 为真则取值 $1$,否则取 $0$。这里考虑二分类问题,且真实目标函数可以是任何函数 $\chi\mapsto\{0,1\}$,函数空间为 $\{0,1\}^{|\chi|}$. 对所有可能的 $f$ 按均匀分布对误差求和,有:
$$
\begin{array}{cc}
\sum_fE_{ote}(Z_a|X,f)=\sum_f\sum_h\sum_{x\in\chi-X}P(x) {II}(h(x)\not ={f(x)}) P(h|X,Z_a)\\ =\sum_{x\in\chi-X}P(x)\sum_hP(h|X,Z_a)\sum_fII(h(x)\not ={f(x)})\\ =\sum_{x\in\chi-X}P(x)\sum_hP(h|X,Z_a)\frac{1}{2}2^{|\chi|}\\ =\frac{1}{2}2^{|\chi|}\sum_{x\in\chi-X}P(x)\sum_hP(h|X,Z_a)\\ =\frac{1}{2}2^{|\chi|}\sum_{x\in\chi-X}P(x)\cdot1
\end{array}
$$
可以看到,上面得出的总误差和学习算法无关,也就是说,不管算法 $Z_a$ 有多聪明,算法 $Z_b$ 有多笨拙,两者期望是相同的。
不过一般认为特征差距小的样本更有可能是同一类。
Summary
机器学习主要分为以下几个步骤:
- 获取训练集;
- 从训练集中提取特征;
- 使用学习算法进行训练;
- 对样本集进行测试。
Support Vector Machine
支持向量机(Vapnik 发明)是一种最大化间隔(Margin)的分类算法。
Linear Model - Linear Separable
定义:
- 训练数据及标记:$\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$,其中 $x$ 为一个向量,$y$ 为一个标记。例如上面提到的
((色泽=青绿, 根蒂=蜷缩, 敲声=浊响), 好瓜); - 线性模型:$(\omega, b)$,其中 $\omega$ 为一个向量(和 $x$ 的维度相同),$b$ 是一个常数。有超平面(Hyperplane)对应的方程 $\omega_1x_1+\omega_2x_2+\cdots+\omega_Nx_N+b=0$,一般写成 $\omega^Tx+b=0$,该超平面将输入空间分成了两个部分,其中超平面的法向量 $\omega=\begin{bmatrix}\omega_1\\ \omega_2\\ \vdots\\ \omega_N\end{bmatrix}$。当学得 $\omega$ 和 $b$ 后,模型就可以确定了;
- 一个训练集($\{(x_i, y_i)\}_{i=1\sim N}$)线性可分是指存在 $(\omega, b)$,对任意 $i=1 \sim N$ 有:
- 若 $y_i=+1$,则 $\omega^Tx_i+b≤0$;
- 若 $y_i=-1$,则 $\omega^Tx_i+b>0$;
- 总结为 $y_i[\omega^Tx_i+b]≥0$。
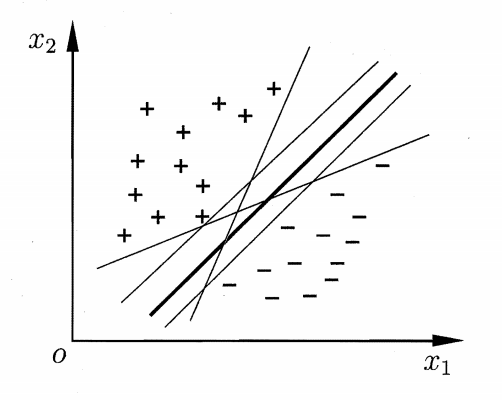
其中使等号成立的点被称为支持向量(Support Vector),两个异类支持向量到超平面的距离称为间隔(Margin)。以下为支持向量机的基本型,即将原本的求最大间隔转换成了一个带有限制条件的最小化问题。同时这里的最小化也是一个优化问题(凸优化问题中的二次规划问题,即目标函数为二次项,而限制条件为一次项,其结果要么无解,要么只有一个极值):
- 最小化(Minimize):$\frac{1}{2}\lVert\omega\rVert^2$;
- 限制条件(Subject to):$y_i[\omega^Tx_i+b]≥1(i=1\sim N)$。
证明:
- 事实 1:$\omega^Tx+b=0$ 与 $a\omega^Tx+ab=0$ 是同一个平面($a\in \mathbb{R}^+$),两者满足同一公式;
- 事实 2:点到平面的距离公式。
- 有平面 $\omega_1x+\omega_2y+b=0$,则点 $(x_0, y_0)$ 到此平面的距离 $d$ 为 $\frac{|\omega_1x_0+\omega_2y_0+b|}{\sqrt{\omega_1^2+\omega_2^2}}$;
- 有超平面 $\omega^Tx+b=0$,则向量 $x_0$ 到此超平面的距离 $d$ 为 $\frac{\omega^Tx_0+b}{\sqrt{\omega_1^2+\omega_2^2+\cdots+\omega_m^2}}$,即 $\frac{\omega^Tx_0+b}{\lVert\omega\rVert}$。
- 可以用 $a$ 去缩放,使得 $(\omega, b)$ 变为 $(a\omega, ab)$,最终使在支持向量 $x_0$ 上有:$|\omega^Tx_0+b|=1$,此时支持向量与平面的距离为 $d=\frac{1}{\lVert\omega\rVert}$。那么最小化 $\lVert\omega\rVert$ 就可以达到最大化间隔 $d$ 的作用(二次方和参数 $\frac{1}{2}$ 主要用于后面的求导,对求最小化没有影响)。
Non-linear Model - Non-linear Separable
对线性模型进行改造:
- 最小化:$\frac{1}{2}\lVert\omega\rVert^2+C\sum_{i=1}^N\xi_i$,$\xi$ 为松弛变量(Slack Variable),$C\sum_{i=1}^N\xi_i$ 为正则项(Regulation Term),$C$ 为事先设定好的参数;
- 限制条件;
- $y_i[\omega^Tx_i+b]≥1-\xi(i=1\sim N)$;
- $\xi≥0$。
- 高维映射 $\phi(x)$,即 $x\mapsto^\phi\phi(x)$,$x$ 是一个低维的矢量,$\phi(x)$ 是一个高维的矢量。
- 在高维空间下被线性分割的概率更大,故可以将原限制条件中的 $x$ 替换为 $\phi(x)$,同时 $\omega$ 也变为一个和 $\phi(x)$ 相同维度的向量;
- 例:有如下高维映射 $x=\begin{bmatrix}a\\ b\end{bmatrix}\mapsto^\phi\phi(x)=\begin{bmatrix}a^2\\ b^2\\ a\\ b\\ ab\end{bmatrix}$
- 给出异或问题如下:$x_1=\begin{bmatrix}0\\ 0\end{bmatrix}\in C_1$、$x_2=\begin{bmatrix}1\\ 1\end{bmatrix}\in C_1$、$x_3=\begin{bmatrix}1\\ 0\end{bmatrix}\in C_2$、$x_4=\begin{bmatrix}0\\ 1\end{bmatrix}\in C_2$;
- 经过上面的高维映射后,得到 $\phi(x_1)=\begin{bmatrix}0\\ 0\\ 0\\ 0\\ 0\end{bmatrix}$、$\phi(x_2)=\begin{bmatrix}1\\ 1\\ 1\\ 1\\ 1\end{bmatrix}$、$\phi(x_3)=\begin{bmatrix}1\\ 0\\ 1\\ 0\\ 0\end{bmatrix}$、$\phi(x_4)=\begin{bmatrix}0\\ 1\\ 0\\ 1\\ 0\end{bmatrix}$;
- 可求出一组 $\omega=\begin{bmatrix}-1\\ -1\\ -1\\ -1\\ 6\end{bmatrix}, b=1$,使得 $\begin{cases}\omega^T\phi(x_1)+b=1\in C_1\\ \omega^T\phi(x_2)+b=3\in C_1\\ \omega^T\phi(x_3)+b=-1\in C_2\\ \omega^T\phi(x_4)+b=-1\in C_2\end{cases}$。
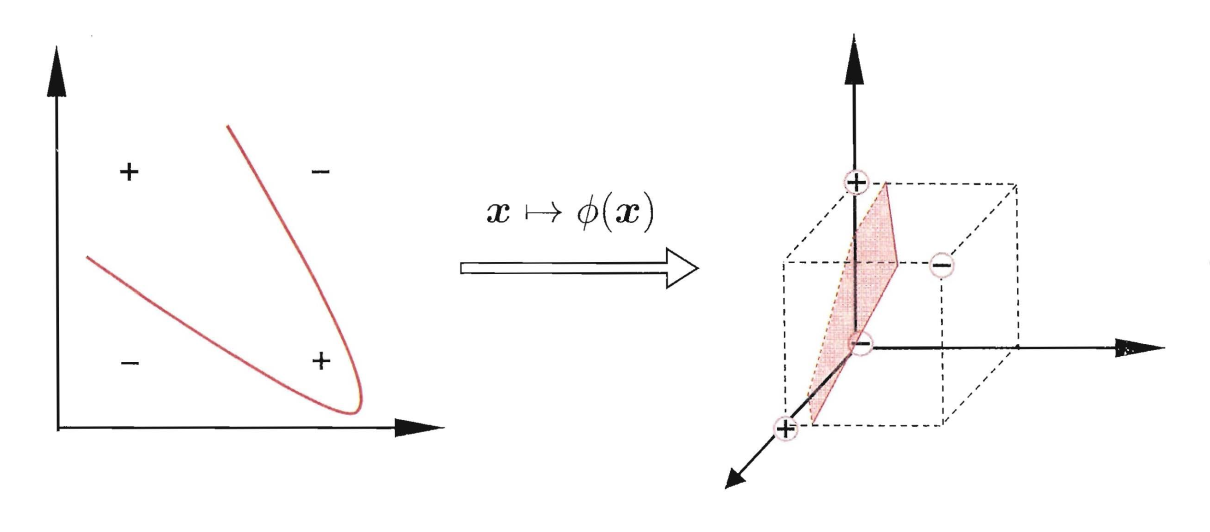
SVM 中将 $\phi(x)$ 选择为无限维映射。而我们可以不知道无限维映射 $\phi(x)$ 的显示表达式,只需要知道一个核函数(Kernel Function)($\phi(x_i)$ 和 $\phi(x_j)$ 两个无限维向量的内积):
$$
K(x_i,x_j)=\phi(x_i)^T\phi(x_j)
$$
则无限维优化式仍然可解。
核函数
| 名称 | 表达式 | 参数 |
|---|---|---|
| 线性核(Linear) | $K(x_i,x_j)=x_i^Tx_j$ | - |
| 多项式核(Poly) | $K(x_i,x_j)=(x_i^Tx_j)^d$ | $d≥1$ 为多项式的次数 |
| 高斯径向基函数(RBF) | $K(x_i,x_j)=e^{-\frac{\lVert x_i-x_j\rVert^2}{2\tau^2}}$ | $\tau>0$ 为高斯核的带宽(Width) |
| 拉普拉斯核 | $K(x_i,x_j)=e^{-\frac{\lVert x_i-x_j\rVert}{\tau}}$ | $\tau>0$ |
| Sigmoid 核 | $K(x_i,x_j)=\tanh(\beta x_i^Tx_j+\theta)$ | $\tanh$ 为双曲正切函数,$\beta>0$,$\theta<0$ |
通过函数组合也可以得到核函数:
- 若 $K_1$ 和 $K_2$ 是核函数,则对于任意正数 $\gamma_1$、$\gamma_2$,其线性组合 $\gamma_1K_1+\gamma_2K_2$ 也是核函数;
- 若 $K_1$ 和 $K_2$ 是核函数,则核函数的直积(笛卡尔积)$K_1\times K_2(x_i,x_j)=K_1(x_i,x_j)K_2(x_i,x_j)$ 也是核函数;
- 若 $K_1$ 是核函数,则对于任意函数 $g(x)$,$K(x_i,x_j)=g(x_i)K_1(x_i,x_j)g(x_j)$ 也是核函数。
$K(x_i,x_j)$ 能够写成 $\phi(x_i)^T\phi(x_j)$ 的充要条件(Mercer’s Theorem):
- 交换性:$K(x_i,x_j)=K(x_j,x_i)$;
- 半正定性:对任意常数 $c_i$ 和向量 $x_i$($i=1\sim N$),有 $\sum_{i=1}^N\sum_{j=1}^Nc_ic_jK(x_i,x_j)≥0$。
优化理论
需要在只知道 $K$,不知道 $\phi$ 的情况下解出优化问题(Kernel Trick)。
原问题(Prime Problem)
- 最小化:$f(\omega)$;
- 限制条件:$g_i(\omega)≤0(i=1\sim K)$、$h_i(\omega)=0(i=1\sim M)$。
对偶问题(Dual Problem)
- 定义函数:$\begin{array}{cc}L(\omega,\alpha,\beta)=f(\omega)+\sum_{i=1}^K\alpha_ig_i(\omega)+\sum_{i=1}^M\beta_ih_i(\omega)\\ =f(\omega)+\alpha^Tg(\omega)+\beta^Th(\omega)\end{array}$;
- 对偶问题定义。
- 最大化:$\theta(\alpha,\beta)=\inf_{所有\omega}\{L(\omega,\alpha,\beta)\}$,其中 $\inf$ 是在确定 $\alpha$ 和 $\beta$ 的情况下遍历 $\omega$ 来计算最小值;
- 限制条件:$\alpha_i≥0(i=1\sim K)$。
原问题和对偶问题之间的关系
定理:如果 $\omega^*$ 是原问题的解,而 $\alpha^*$、$\beta^*$ 是对偶问题的解,则有:
$$
f(\omega^*)≥\theta(\alpha^*,\beta^*)
$$
证:
$$
\begin{array}{cc}
\theta(\alpha^*,\beta^*)=\inf\{L(\omega,\alpha^*,\beta^*)\}\\ ≤L(\omega^*,\alpha^*,\beta^*)\\ =f(\omega^*)+\sum_{i=1}^K\alpha_i^*g_i(\omega^*)+\sum_{i=1}^M\beta_i^*h_i(\omega^*)\\ ≤f(\omega^*)
\end{array}
$$
- 定义:$G=f(\omega^*)-\theta(\alpha^*,\beta^*)≥0$,其中 $G$ 叫做原问题与对偶问题的间距(Duality Gap);
- 对于某些特定的优化问题,可以证明 $G=0$;
- 强对偶定理:若 $f(\omega)$ 是凸函数,且 $g(\omega)=A\omega+b$,$h(\omega)=C\omega+d$,则此优化问题的原问题与对偶问题的间距为 0,即当 $\omega^*$ 是原问题的解,而 $\alpha^*$、$\beta^*$ 是对偶问题的解时,满足 $f(\omega^*)=\theta(\alpha^*,\beta^*)$;
- KKT 条件(Karush–Kuhn–Tucker Condition):在强对偶定理的条件下,对于任意的 $i=1\sim K$,可以得到 $\alpha_i^*=0$ 或 $g_i^*(\omega^*)=0$。
证明非线性模型
为了和原问题一一对应,将 SVM 做以下调整:
- 最小化:$f(\omega)=\frac{1}{2}\lVert\omega\rVert^2-C\sum_{i=1}^N\xi_i$(凸函数);
- 凸函数定义:对任意 $\omega_1$、$\omega_2$、$\lambda\in[0,1]$,满足 $f(\lambda\omega_1+(1-\lambda)\omega_2)≤\lambda f(\omega_1)+(1-\lambda)f(\omega_2)$。
- 限制条件;
- $1+\xi_i-y_i\omega^T\phi(x_i)+y_ib≤0$;
- $\xi_i≤0$($i=1\sim K$)。
接下来写出对应的对偶问题:
- 最大化:$\begin{array}{cc}\theta(\alpha,\beta)=\\ \inf_{所有(\omega,\xi_i,b)}\{\frac{1}{2}\lVert\omega\rVert^2-C\sum_{i=1}^N\xi_i+\sum_{i=1}^N\beta_i\xi_i+\sum_{i=1}^N\alpha_i[1+\xi_i-y_i\omega^T\phi(x_i)-y_ib]\}\end{array}$;
- 限制条件($i=1\sim N$)。
- $\alpha_i≥0$;
- $\beta_i≥0$。
接下来将对偶问题中的最大化进行化简。首先计算 $\inf$ 对应的最小值,需要求三个自变量对应的偏导数:
$$
\begin{cases}
\frac{\partial L}{\partial\omega}=0\\
\frac{\partial L}{\partial\xi_i}=0\\
\frac{\partial L}{\partial b}=0
\end{cases}
$$
- 其中对向量 $\omega=\begin{bmatrix}\omega_1\\ \omega_2\\ \vdots\\ \omega_m\end{bmatrix}$ 求 $f(\omega)$ 的偏导相当于对每一个分量求偏导,即 $\frac{\partial f}{\partial\omega}=\begin{bmatrix}\frac{\partial f}{\partial\omega_1}\\ \frac{\partial f}{\partial\omega_2}\\ \vdots\\ \frac{\partial f}{\partial\omega_m}\end{bmatrix}$;
- 若 $f(\omega)=\frac{1}{2}\lVert\omega\rVert^2$,则 $\frac{\partial f}{\partial\omega}=\omega$;
- 若 $f(\omega)=\omega^Tx$,则 $\frac{\partial f}{\partial\omega}=x$。
求三个自变量的偏导数的结果如下:
$$
\begin{cases}
\frac{\partial L}{\partial\omega}=0 \mapsto \omega-\sum_{i=1}^N\alpha_iy_i\phi(x_i)=0\\
\frac{\partial L}{\partial\xi_i}=0 \mapsto -C+\beta_i+\alpha_i=0\\
\frac{\partial L}{\partial b}=0 \mapsto -\sum_{i=1}^N\alpha_iy_i=0
\end{cases}
$$
接着将求出的条件代入 $\theta(\alpha,\beta)$,将 $\frac{1}{2}\lVert\omega\rVert^2$ 化简,可以消去 $\phi(\cdot)$:
$$
\begin{array}{cc}
\frac{1}{2}\lVert\omega\rVert^2=\frac{1}{2}\omega^T\omega\\
=\frac{1}{2}(\sum_{i=1}^N\alpha_iy_i\phi(x_i))^T(\sum_{j=1}^N\alpha_jy_j\phi(x_j))\\
=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)\\
=\frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)
\end{array}
$$
同理可以把 $-\sum_{i=1}^N\alpha_iy_i\omega^T\phi(x_i)$ 化简,并消去 $\phi(\cdot)$:
$$
\begin{array}{cc}
-\sum_{i=1}^N\alpha_iy_i\omega^T\phi(x_i)=-\sum_{i=1}^N\alpha_iy_i(\sum_{j=1}^N\alpha_jy_j\phi(x_j))^T\phi(x_i)\\
=-\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_j\phi(x_j)^T\phi(x_i)\\
=-\sum_{i=1}^N\sum_{j=1}^N\alpha_i\alpha_jy_iy_jK(x_i,x_j)
\end{array}
$$
最后得到对偶问题的最终式:
- 最大化:$\begin{array}{cc}\theta(\alpha)=\frac{1}{2}\lVert\omega\rVert^2+\sum_{i=1}^N\alpha_i[1-y_i\omega^T\phi(x_i)]\\ =\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}\sum_{j=1}\alpha_i\alpha_jy_iy_jK(x_i,x_j)\end{array}$;
- SMO 算法可以解凸优化问题。
- 限制条件。
- $0≤\alpha_i≤C$;
- $\sum_{i=1}^N\alpha_iy_i=0$。
这里最终得到的是一个有关 $\alpha$ 的优化问题。由于测试时需要计算 $\omega^T\phi(x_i)+b$ 的值,所以这里仍然需要找到 $\omega^T\phi(x_i)+b$ 和 $\alpha$ 之间的关系。首先 $\omega$ 不需要计算,可以通过和前面类似的方法,使用核函数计算出 $\omega^T\phi(x_i)$ 的值:
$$
\begin{array}{cc}
\omega^Tx_i=(\sum_{j=1}^N\alpha_jy_j\phi(x_j))^T\phi(x_i)\\
=\sum_{j=1}^N\alpha_jy_j\phi(x_j)^T\phi(x_i)\\
=\sum_{j=1}^N\alpha_jy_jK(x_i,x_j)
\end{array}
$$
接下来是 $b$。因为这里的情况满足 KKT 条件,那么存在 $\alpha_i^*=0$ 或是 $g_i^*(\omega^*)=0$,对应满足的式子如下:
- 要么 $\beta_i=0$;要么 $\xi_i=0$;
- 要么 $\alpha_i=0$;要么 $1+\xi_i-y_i\omega^T\phi(x_i)-y_ib=0$。
首先取一个 $0<\alpha_i<C$,那么 $1+\xi_i-y_i\omega^T\phi(x_i)-y_ib=0$,同时可得出 $\beta_i=C-\alpha_i>0$,即 $\beta_i≠0$ 且 $\xi_i=0$。经化简后,$b$ 的值为:
$$
\begin{array}{cc}
1-y_i\omega^T\phi(x_i)-y_ib=0\\
b=\frac{1-y_i\omega^T\phi(x_i)}{y_i}\\
b=\frac{1-y_i(\sum_{j=1}^N\alpha_jy_j\phi(x_j))^T\phi(x_i)}{y_i}\\
b=\frac{1-y_i\sum_{j=1}^N\alpha_jy_jK(x_i,x_j)}{y_i}
\end{array}
$$
Summary
- 训练流程;
- 输入训练样本 $\{(x_i,y_i)\}_{i=1\sim N}$;
- 解优化问题。
- 最大化:$\theta(\alpha)=\sum_{i=1}^N\alpha_i-\frac{1}{2}\sum_{i=1}\sum_{j=1}\alpha_i\alpha_jy_iy_jK(x_i,x_j)$;
- 限制条件。
- $0≤\alpha_i≤C$;
- $\sum_{i=1}^N\alpha_iy_i=0$。
- 算 $b$,找一个 $0<\alpha_i<C$,得出 $b=\frac{1-y_i\sum_{j=1}^N\alpha_jy_jK(x_i,x_j)}{y_i}$。
- 测试流程。
- 输入测试样本 $X$。
- 若 $\sum_{i=1}^N\alpha_iy_iK(x_i,x)+b≥0$,则 $y=+1$;
- 若 $\sum_{i=1}^N\alpha_iy_iK(x_i,x)+b<0$,则 $y=-1$。
- 输入测试样本 $X$。
Programming
- 兵王问题:黑方只剩一个王,白方剩一个兵一个王;
- 两种可能;
- 白方将死黑方,获胜;
- 和棋。
- 这两种可能视三个棋子在棋盘的位置而确定。
有数据 krkopt.data 用于训练和测试。每行为一组数据集和标记,前 6 位是 3 个坐标,最后一个单词表示平局(draw)或是白棋在 x 步之后将死黑棋:
$ wc krkopt.data
28056 28056 531806 krkopt.data
$ cat ./krkopt.data
a,1,b,3,c,2,draw
a,1,c,1,c,2,draw
a,1,c,1,d,1,draw
a,1,c,1,d,2,draw
a,1,c,2,c,1,draw
a,1,c,2,c,3,draw
a,1,c,2,d,1,draw
a,1,c,2,d,2,draw
a,1,c,2,d,3,draw
a,1,c,3,c,2,draw
...
c,3,e,6,e,1,nine
c,3,e,6,f,1,nine
c,3,e,6,g,1,nine
c,3,e,6,h,2,nine
c,3,e,6,h,7,nine
c,3,e,7,e,1,nine
c,3,e,7,f,1,nine
c,3,e,7,g,1,nine
c,3,e,7,h,2,nine
c,3,e,8,e,1,nine
c,3,e,8,f,1,nine
...
b,1,g,3,e,4,sixteen
b,1,g,3,e,5,sixteen
b,1,g,3,f,5,sixteen
b,1,g,3,g,5,sixteen
b,1,g,6,e,4,sixteen
b,1,g,6,e,5,sixteen
b,1,g,6,e,6,sixteen
b,1,g,6,f,4,sixteen
b,1,g,6,g,4,sixteen
b,1,g,7,e,5,sixteen
b,1,g,7,e,6,sixteen
- 总样本数 28056,其中正样本 2796,负样本 25260;
- 随机取 5000 个样本进行训练,其余用于测试;
- 样本归一化,在训练样本上,求出每个维度的均值和方差,在训练和测试样本上同时归一化:$newX=\frac{X-mean(X)}{std(X)}$,其中 $mean(X)$ 是 $X$ 的均值,$std(X)$ 是 $X$ 方差的二次根;
- 高斯核;
- 5-Fold Cross Validation,在 $CScale=[2^{-5}, 2^{15}]$、$\gamma Scale=[2^{-15},2^3]$ 中遍历求识别率的最大值。
LIBSVM
LIBSVM 是台湾林智仁教授在 2001 年开发的一套支持向量机的库,可以很方便的对数据做分类或回归。由于 LIBSVM 程序小,运用灵活,输入参数少,并且是开源的,易于扩展,其成为目前国内应用最多的 SVM 的库。这里使用 Python 下的 libsvm 库进行测试:
$ python3 -m pip install --user libsvm -U
训练参数设置:svmtrain(yTraining, xTraining, cmd),cmd 的参数设置如下:
-s svm_type: set type of SVM (default 0)0 -- C-SVC (multi-class classification)1 -- nu-SVC (multi-class classification)2 -- one-class SVM3 -- epsilon-SVR (regression)4 -- nu-SVR (regression)
-t kernel_type: set type of kernel function (default 2)0 -- linear1 -- polynomial2 -- radial basis function3 -- sigmoid4 -- precomputed kernel
-c cost: set the parameter C of C-SVC, epsilon-SVR, and nu-SVR (default 1)-g gamma: set gamma in kernel function (default 1/num_features)-v n: n-fold cross validation mode
先尝试用在 Github 上的项目给的例子 heart_scale 熟悉一下基本的函数。大概可以分析出 libsvm 可以直接读取的训练样本的格式,第一列为标记(Label),后面的数据集以 Index:Value 的形式排列:
$ head heart_scale
+1 1:0.708333 2:1 3:1 4:-0.320755 5:-0.105023 6:-1 7:1 8:-0.419847 9:-1 10:-0.225806 12:1 13:-1
-1 1:0.583333 2:-1 3:0.333333 4:-0.603774 5:1 6:-1 7:1 8:0.358779 9:-1 10:-0.483871 12:-1 13:1
+1 1:0.166667 2:1 3:-0.333333 4:-0.433962 5:-0.383562 6:-1 7:-1 8:0.0687023 9:-1 10:-0.903226 11:-1 12:-1 13:1
-1 1:0.458333 2:1 3:1 4:-0.358491 5:-0.374429 6:-1 7:-1 8:-0.480916 9:1 10:-0.935484 12:-0.333333 13:1
-1 1:0.875 2:-1 3:-0.333333 4:-0.509434 5:-0.347032 6:-1 7:1 8:-0.236641 9:1 10:-0.935484 11:-1 12:-0.333333 13:-1
-1 1:0.5 2:1 3:1 4:-0.509434 5:-0.767123 6:-1 7:-1 8:0.0534351 9:-1 10:-0.870968 11:-1 12:-1 13:1
+1 1:0.125 2:1 3:0.333333 4:-0.320755 5:-0.406393 6:1 7:1 8:0.0839695 9:1 10:-0.806452 12:-0.333333 13:0.5
+1 1:0.25 2:1 3:1 4:-0.698113 5:-0.484018 6:-1 7:1 8:0.0839695 9:1 10:-0.612903 12:-0.333333 13:1
+1 1:0.291667 2:1 3:1 4:-0.132075 5:-0.237443 6:-1 7:1 8:0.51145 9:-1 10:-0.612903 12:0.333333 13:1
+1 1:0.416667 2:-1 3:1 4:0.0566038 5:0.283105 6:-1 7:1 8:0.267176 9:-1 10:0.290323 12:1 13:1
使用 svm_read_problem 读取标记和数据集,使用 svm_train 训练指定数据,并最后使用 svm_predict 进行测试数据:
#!/usr/bin/env python3
from libsvm.svmutil import *
y, x = svm_read_problem('./heart_scale') # 获取全部的标记和数据集
m = svm_train(y[:200], x[:200], '-c 4') # 对前200组数据进行训练,并采用
p_label, p_acc, p_val = svm_predict(y[200:], x[200:], m) # 对200组之后所有的数据进行测试
训练的效果如下,在剩下的 70 组数据中测试的正确率为 84.2857%:
$ ./heart_scale.py
*.*
optimization finished, #iter = 257
nu = 0.351161
obj = -225.628984, rho = 0.636110
nSV = 91, nBSV = 49
Total nSV = 91
Accuracy = 84.2857% (59/70) (classification)
接下来是对兵王问题的训练和测试。这里的数据在读取时需要做一点处理,全部转换成数字。中间训练的过程就是寻找较为准确的 $C$ 和 $\gamma$ 的过程(归一化、缩小范围)。最后使用生成的模型进行测试:
#!/usr/bin/env python3
from libsvm.svmutil import *
from operator import itemgetter
import numpy as np
import random
def readData(filename): # 读取数据
xApp = []
yApp = []
with open(filename, 'rb') as f:
data = f.readlines()
for l in data:
t = l.split(b',')
# 二分类问题
if t[-1].startswith(b'draw'):
y = 0 # 平局为0
else:
y = 1 # 胜出为1
del t[-1]
# 把字母转化为数字
xs = [int(c) if ord(c) < 0x3a and ord(c) > 0x2f else ord(c) - ord('a') for c in t]
xApp.append(xs)
yApp.append(y)
return yApp, xApp
def dealWithData(yApp, xApp, trainingDataLength): # 处理数据
xTraining = []
yTraining = []
xTesting = []
yTesting = []
idxs = list(range(len(xApp)))
random.shuffle(idxs) # 打乱数据
for i in range(trainingDataLength):
xTraining.append(xApp[idxs[i]])
yTraining.append(yApp[idxs[i]])
for i in range(trainingDataLength, len(xApp)):
xTesting.append(xApp[idxs[i]])
yTesting.append(yApp[idxs[i]])
avgX = np.mean(np.mat(xTraining), axis=0).tolist()[0] # 计算训练数据集各个维度的算术平均值
stdX = np.std(np.mat(xTraining), axis=0).tolist()[0] # 计算训练数据集各个维度的标准方差
print('[*] avgX = ' + str(avgX))
print('[*] stdX = ' + str(stdX))
# 样本归一化
for data in xTraining:
for i in range(len(data)):
data[i] = (data[i] - avgX[i]) / stdX[i]
for data in xTesting:
for i in range(len(data)):
data[i] = (data[i] - avgX[i]) / stdX[i]
return yTraining, xTraining, yTesting, xTesting
def trainingModel(label, data, modelFilename): # 训练模型
CScale = [-5, -3, -1, 1, 3, 5, 7, 9, 11, 13, 15]
gammaScale = [-15, -13, -11, -9, -7, -5, -3, -1, 1, 3]
maxRecognitionRate = 0
maxC = 0
maxGamma = 0
for C in CScale:
C_ = pow(2, C)
for gamma in gammaScale:
gamma_ = pow(2, gamma)
cmd = '-t 2 -c ' + str(C_) + ' -g ' + str(gamma_) + ' -v 5 -q'
recognitionRate = svm_train(label, data, cmd)
# 比较获取准确率最高的C和gamma
if recognitionRate > maxRecognitionRate:
maxRecognitionRate = recognitionRate
maxC = C
maxGamma = gamma
n = 10
minCScale = 0.5 * (min(-5, maxC) + maxC)
maxCScale = 0.5 * (max(15, maxC) + maxC)
newCScale = np.arange(minCScale, maxCScale+1, (maxCScale-minCScale)/n)
print('[*] newCScale = ' + str(newCScale))
minGammaScale = 0.5 * (min(-15, maxGamma) + maxGamma)
maxGammaScale = 0.5 * (max(3, maxGamma) + maxGamma)
newGammaScale = np.arange(minGammaScale, maxGammaScale+1, (maxGammaScale-minGammaScale)/n)
print('[*] newGammaScale = ' + str(newGammaScale))
for C in newCScale:
C_ = pow(2, C)
for gamma in newGammaScale:
gamma_ = pow(2, gamma)
cmd = '-t 2 -c ' + str(C_) + ' -g ' + str(gamma_) + ' -v 5 -q'
recognitionRate = svm_train(label, data, cmd)
# 比较获取准确率最高的C和gamma
if recognitionRate > maxRecognitionRate:
maxRecognitionRate = recognitionRate
maxC = C
maxGamma = gamma
# 使用最终确定的C和gamma训练模型
print('[*] maxC = ' + str(maxC))
print('[*] maxGamma = ' + str(maxGamma))
C = pow(2, maxC)
gamma = pow(2, maxGamma)
cmd = '-t 2 -c ' + str(C) + ' -g ' + str(gamma)
model = svm_train(label, data, cmd)
svm_save_model(modelFilename, model)
return model
if __name__ == '__main__':
yApp, xApp = readData('krkopt.data')
yTraining, xTraining, yTesting, xTesting = dealWithData(yApp, xApp, 5000)
if input('Train or not? (y/n) ') == 'y':
model = trainingModel(yTraining, xTraining, 'krkopt.model')
else:
model = svm_load_model('krkopt.model')
yPred, accuracy, decisionValues = svm_predict(yTesting, xTesting, model)
最后测试的结果大约为 99.4492%:
$ ./testSVMChessLibSVM.py
[*] avgX = [2.0886, 1.8438, 3.5566, 4.557, 3.9804, 4.4256]
[*] stdX = [0.9459122792309963, 0.9203268767128373, 2.291548917217361, 2.2831449800658565, 2.3259440749940588, 2.265582627052049]
Train or not? (y/n) y
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
...
Cross Validation Accuracy = 89.9%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 90.08%
Cross Validation Accuracy = 99.26%
Cross Validation Accuracy = 99.32%
Cross Validation Accuracy = 99.18%
Cross Validation Accuracy = 98.56%
Cross Validation Accuracy = 98.56%
Cross Validation Accuracy = 95.46%
Cross Validation Accuracy = 89.88%
[*] newCScale = [ 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13.]
[*] newGammaScale = [-10. -9.1 -8.2 -7.3 -6.4 -5.5 -4.6 -3.7 -2.8 -1.9 -1. -0.1]
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 89.58%
Cross Validation Accuracy = 90.62%
Cross Validation Accuracy = 96.2%
Cross Validation Accuracy = 98.5%
Cross Validation Accuracy = 98.92%
Cross Validation Accuracy = 98.7%
...
Cross Validation Accuracy = 98.28%
Cross Validation Accuracy = 99.2%
Cross Validation Accuracy = 99.24%
Cross Validation Accuracy = 99.28%
Cross Validation Accuracy = 99.34%
Cross Validation Accuracy = 99.16%
Cross Validation Accuracy = 98.94%
Cross Validation Accuracy = 98.76%
Cross Validation Accuracy = 98.76%
Cross Validation Accuracy = 98.86%
Cross Validation Accuracy = 97.9%
[*] maxC = 11
[*] maxGamma = -5
...............................................................................................................*........................................................................................................................................................................*................................................................................................*
optimization finished, #iter = 375498
nu = 0.033157
obj = -251795.371532, rho = -81.180115
nSV = 228, nBSV = 110
Total nSV = 228
Accuracy = 99.4492% (22929/23056) (classification)
混淆矩阵
- TP(True Positive):将正样本识别为正样本的数量(或概率);
- FN(False Negative):将正样本识别为负样本的数量(或概率);
- FP(False Positive):将负样本识别为正样本的数量(或概率);
- TN(True Negative):将负样本识别为负样本的数量(或概率)。
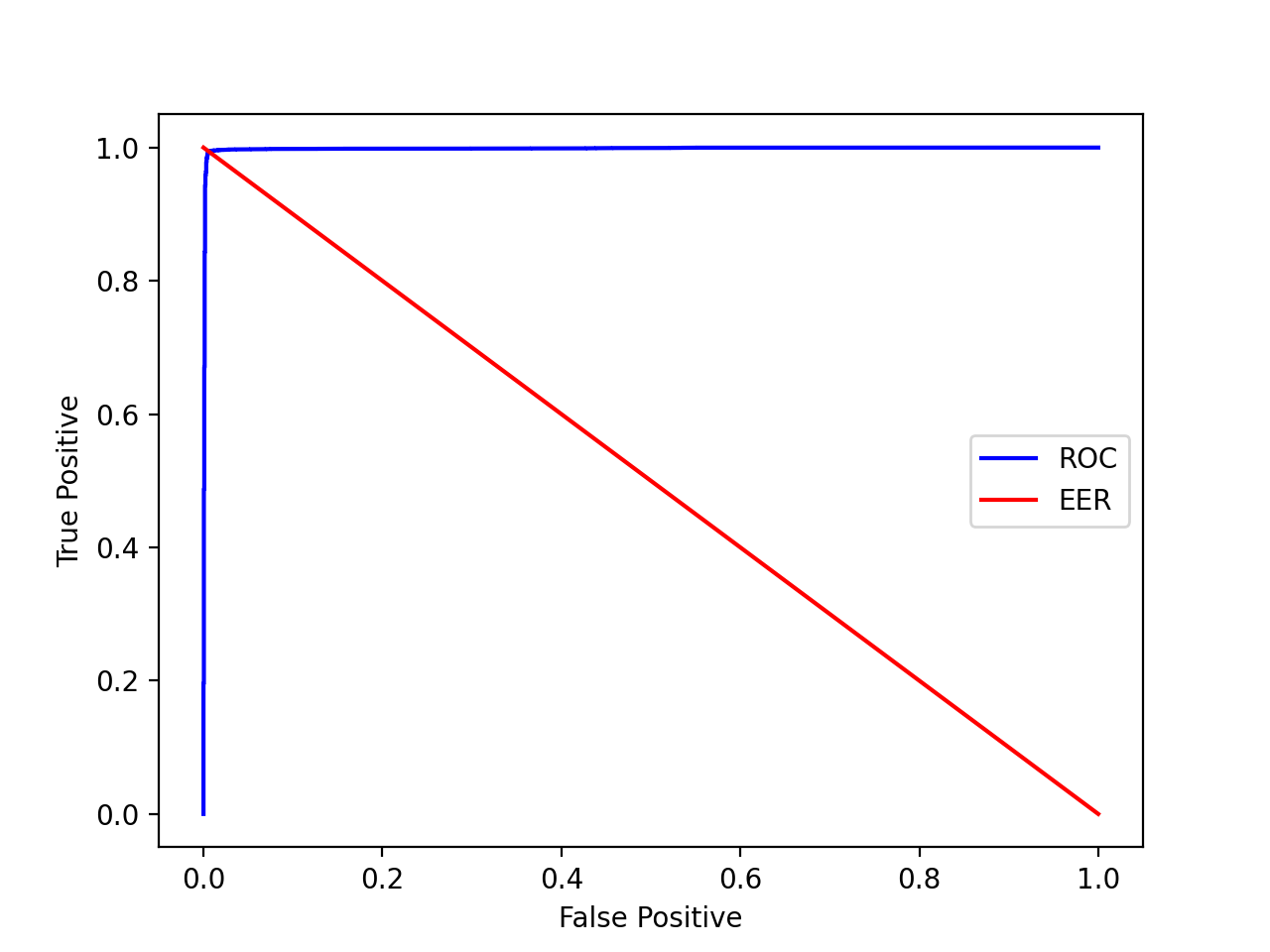
ROC(Receiver Operating Charactor)曲线
ROC 曲线是一条横坐标 FP,纵坐标 TP 的曲线。四个概率 TP、FN、FP、TN 的关系:
- $TP+FN=1$;
- $FP+TN=1$;
- 对同一个系统来说,若 $TP$ 增加,则 $FP$ 也增加;
- 在 FP 为 0 的情况下,TP 的值越高则系统性能越好。
等错误率(Equal Error Rate)是两类错误 FP 和 FN 相等时候的错误率,可以直观地表示系统性能。以上面兵王问题画出的 ROC 曲线和 ERR 为例:
#!/usr/bin/env python3
# ...
import matplotlib.pyplot as plt
# ...
def drawROC(yTesting, decisionValues): # 绘制ROC曲线
values, labels = [list(x) for x in zip(*sorted(zip(decisionValues, yTesting), key=itemgetter(0)))]
truePositive = [0 for i in range(len(values) + 1)]
trueNegative = [0 for i in range(len(values) + 1)]
falsePositive = [0 for i in range(len(values) + 1)]
falseNegative = [0 for i in range(len(values) + 1)]
for i in range(len(values)):
if labels[i] == 1:
truePositive[0] += 1
else:
falsePositive[0] += 1
for i in range(len(values)):
if labels[i] == 1:
truePositive[i + 1] = truePositive[i] - 1
falsePositive[i + 1] = falsePositive[i]
else:
falsePositive[i + 1] = falsePositive[i] - 1
truePositive[i + 1] = truePositive[i]
truePositive = (np.array(truePositive) / truePositive[0]).tolist()
falsePositive = (np.array(falsePositive) / falsePositive[0]).tolist()
plt.xlabel('False Positive')
plt.ylabel('True Positive')
plt.plot(falsePositive, truePositive, color='blue') # ROC
plt.plot([1,0], [0,1], color='red') # EER
plt.legend(['ROC', 'EER'])
plt.show()
if __name__ == '__main__':
# ...
drawROC(yTesting, decisionValues)
SVM 处理多分类问题
SVM 有三种方式处理多类问题,即类别大于 2 的问题:
- 改造优化的目标函数和限制条件,使之能处理多类问题;
- 一类对其他类;
- 一类对另一类。
References
《机器学习》——周志华
浙江大学信电学院《机器学习》课程